Blockset described on this wiki is deprecated since 2012.
For Model Based Design (MBD), use the free MPLAB Device Blocks for Simulink, tool from Microchip.
Updated Rapid Control Prototyping (RCP) custom projects are published at: https://lubin.kerhuel.eu.
Miniature Inertial Measurement Unit - IMU
Implementation of a miniature Inertial Measurement Unit (IMU) on a dsPIC microcontroller with Mathworks (tm) rapid prototyping tools coupled with the dsPIC blockset. Simulink is used to both simulate and generate the embedded software that is downloaded onboard the dsPIC microcontroller. This IMU estimates pitch and roll angles using two different types of Micro Electro Mechanical Systems (MEMS) sensors: rate gyro and accelerometers.
All files: simulink model, matlab script and data files (.mat) can be downloaded from the Download section at the bottom of this page.
Contents
- 1 Introduction
- 2 Problems of angles estimation from inertial sensors
- 3 IMU based on a 5 DoF sensor board (2 rate gyro, 3 accelerometers)
- 4 IMU based on a 6 DoF sensor board (3 rate gyro, 3 accelerometers)
- 5 Acknowledgement
Introduction
The micro Inertial Measurement Unit (IMU) It is an attitude indicator (ADI) or artificial horizon also called gyro horizon that estimates its attitude about both axis: pitch and roll. The electronics parts are:
- 3 Rate gyros measuring roll, pitch and yaw speed rate (yaw measurement with 6DoF sensor board only)
- 1 tri axial accelerometer measuring both the IMU acceleration and the earth gravity
- 1 dsPIC (could be either 30f, 33f or a PIC24) for the embedded calculation tasks
The first part settle the inherent problem of angle estimation from inertial sensors using MEMS. Then, a first IMU based on a 5 DoF sensor board is presented. Its sensor board is described. Raw data measurement are recorded and different data fusing algorithms are compared with simulation based on the real data previously recorded. The implementation of the simulink model using a dsPIC is then described. I am using extensively the rapid prototyping tool described on this website (dsPIC blockset for Simulink) allowing generating the .hex code file for the microcontroller directly from the simulink model file (previously simulated) with a one push button procedure. Limitation of this 5DoF sensor board is explained and an IMU algorithm using a 6 DoF sensor board is presented and implemented
Problems of angles estimation from inertial sensors
Estimating angles from rate gyro
A rate gyro measures its angular speed rate. Precision of theses MEMS sensors are usually good. Thus, integrating the value of the rate gyro over time provide a good estimation of the angular displacement. Provided the initial position of the system is known and the sensor has a zero mean noise, an integration will provides the angular orientation. The integration process also acts as a low pass filter and reduce the high frequency noise (despite the fact theses sensors has already low noise).
- [math]\Theta[/math] the absolute pitch angle and q the pitch angular rate.
[math]\hat \Theta(t) = \int_{t_0}^t{q(t) dt}+\Theta(t_0)[/math]
- [math]\Phi[/math] the absolute roll angle and p the roll angular rate.
[math]\hat \Phi(t) = \int_{t_0}^t{p(t) dt} + \Phi(t_0)[/math]
Unfortunately, the rate gyro sensor is not ideal. Integrating the rate gyro also integrate its DC value(bias) or its non zero mean noise. The integration of this error introduced a growing error on the estimated angle. As the gyro's DC value drifts slowly over time, it is not possible to cancel this bias by subtracting this DC offset value to the gyro output. Thus, Integration of a rate gyro results in an angular drift which is about 1° per minute (strongly depending on the rate gyro used!). It is necessary to use another sensor so as to recover the gyro bias and correcting for the angle error introduced by the integration process.
Estimating angles from accelerometers
Accelerometers measures both the acceleration and gravity induced forces (From Wikipedia definition). Accelerometers are usually quite noisy and needs to be filtered. In many situation, (induced force of) acceleration of a system could be considered as small compared to the gravity (induced force). If the system do not changes its velocity and orientation, (Hovering helicopters, plane in straight flight...), it is possible to extract the pitch and roll absolute angle using the measured gravity vector.
Let's consider:
- ax the acceleration measured with the accelerometer on the x axis (longitudinal)
- ay the acceleration measured with the accelerometer on the y axis (lateral)
- az the acceleration measured with the accelerometer on the z axis (vertical)
Using the acceleration vector (i.e. gravity) measured with the accelerometers, we get the [math]\Theta[/math] and [math]\Phi[/math] angles :
- [math]\hat \Theta= \arctan \left( \frac{a_z}{a_x} \right)[/math]
- [math]\hat \Phi = \arctan \left( \frac{a_z}{a_y} \right)[/math]
Note than when the axis az and ay are in the horizontal plane, the result is undefined. But pitch or roll angle is not defined as well (eg: a plane which has its nose in the sky, perpendicular to the horizontal has its roll angle undefined). Calibration of the accelerometers gain is not necessary because a fraction is calculated within the trigonometric arctan function. The only point to care about is the gain and offset of all the three axes that must be equal.
However, the first weakness of the angle estimated from accelerometers is its sensibility to the acceleration of the system. In others words, the estimated angle is biased whenever the system accelerates (i.e. change its velocity or its direction). The second weakness is the noisy result that comes from the accelerometers sensors itself. This noise is even greater when the accelerometers sensor is placed onboard a vibrating vehicle (vibration from motors and propellers for plane and helicopters and vibration from displacement from wheeled vehicle). Low pass filtering may lower the noise from vibration but would correct the bias due to the system own acceleration. Adding to this, the low pass filter would add a phase (i.e. delay) that may be prejudicial in an Auto-Pilot feedback loop.
Merging estimation from accelerometers and rate gyro
Angle estimation from either a rate gyro alone or an accelerometer alone does not provide good results. However, the characteristics of these two types of sensors are complementary:
- Gyros provide a clean estimation of angular change in dynamic situation (within a short time range)
- Accelerometers provide a noisy but absolute angle reference in static situation
It is therefore possible to design a data fusion algorithm that merges the static reference angle computed from the accelerometers with the dynamic angle variation estimated from the rate gyro. If the system is regularly subject to high acceleration, the estimated angle should rely mostly on the rate gyro so as to remove the errors induced by the acceleration. Otherwise, the estimated angle could rely more on the accelerometers.
We have the following trade-off:
- The more the angle estimation rely on the accelerometers, the more the angle estimation is subjected to error due to own body acceleration and to noise (from accelerometers sensor)
- The more the angle estimation relies on the rate gyro, the longer the correction time for the final value catch-up the real angle value (Thus less robust to error; for example at initialisation time or when one of the rate gyro saturates).
Thus, the fusion algorithm should take into account the dynamic characteristics of the system.
IMU based on a 5 DoF sensor board (2 rate gyro, 3 accelerometers)
Embedded Electronics
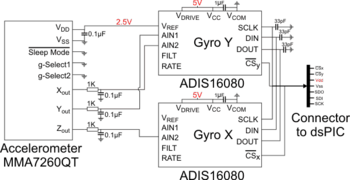
The Embedded IMU Schematic is equipped with one three axis accelerometer MMA7260QT coupled with two one axis rate gyro ADIS16080 (see fig:IMU_SensorSchematic). This custom made board could be replaced by a commercial one like the SEN-00741 from Sparkfun called IMU 5 Degrees of Freedom.
The overall sensor board is supplied with a single stabilized 5V generated with a microchip MCP1252-33X50 component. The 2.5V alimentation required by the accelerometer chip is provided by the 2.5V voltage reference of one rate gyro. The low current required for the accelerometers does not disturb the rate gyro. Each rate gyro has two unused analog input. Thus, the two gyros have 4 analog input, 3 of which are used to convert the three analog values ax, ay, and az from the accelerometer. This sensor board transmits the 5 measurements (3 acceleration + 2 rate gyros) to the microcontroller through a digital SPI bus.
Log raw data from the 5 DoF sensor board
Data from the inertial sensors are logged with matlab. Theses real data feeds a simulink model allowing to develop/debug/compare different data fusion algorithm.
All sensor data are received through the SPI peripheral of the dsPIC. Data are received from the two gyros using the SPI Input/Output interrupt driven block. The code generated by this block is interrupt based. Thus, interruption that continuously occurs allows updating the 2 angular rates and the 3 acceleration measurement. At least, five interrupt must occurs within one model time step (1ms here) to get all values updated. Each block's output the last value received for the corresponding output through the SPI bus.
The dsPIC used (dsPIC 30f4012) run with a 10 Mhz quartz. This frequency allows using the UART at 115 200 bps which is the max baud rate available on most personal computers (Serial port's limitation).
Data are transmitted to the PC through the dsPIC UART peripheral. We have the constraints:
- model time-step is 1ms
- UART speed rate is 115 200 bps
- 5 values (2 from Gyro and 3 from accelerometers) of 12 bits resolution must be transmitted
Two data logging methods are developed: The first logging method uses the Tx Output Multiplexed for Matlab-Labview block. It is the easiest method for viewing and recording variable evolution from a dsPIC. The second method uses the Tx Output block. This last method presented allows recording/viewing more data within one time-step. Both logging method use the graphical matlab interface developed: Interface Tx-Matlab
Using the UART Tx Output Multiplexed for Matlab-Labview block
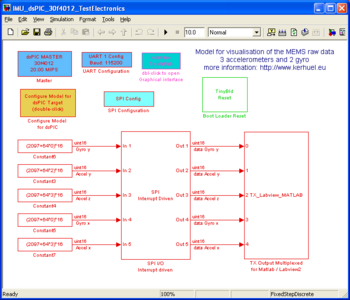
The model IMU_LogData is compiled and the generated .hex file is loaded into the dsPIC (using the bootloader tinybld). The model sampling time is 1 Khz, corresponding to the time-step of 1ms. During 1ms, the UART can send 11,52 bytes when configured at 115200 bps (taking into account the start and stop bits). We log 5 int16 data that is a total of 10 bytes. The multiplexing protocol of the Tx Output Multiplexed for Matlab-Labview block]] adds one byte for each variable sent. Thus, the model should transmit 15 bytes through the UART at each time step. Because the simulink model try to send more than 11 bytes per time-step, some data will not be sent and will be lost. The Intelligent Spreading option will spread the data loss over all channels allowing to view all curves on the graph (If not checked, the two last channels may never be sent).
Because of the lost of some data, this method is easy and great for plotting data. It allows checking that all components are working. It is Not OK to use these data to feed a Simulink model! (You may interpolate the data but it is a bit tricky…)
The data that get out from the Tx Output Multiplexed for Matlab-Labview block are the sensor raw data. It is 16 bits data but only the 12 lower bits contains the measured value.
The dsPIC is connected to the PC COM port (using an equivalent to Max232 component for level translation) and data are logged using the graphical user interface. The following lines are typed at the maltab prompt to save data into a .mat file:
>> [R T] = padr(Rn,1,t_Rn); % remove NaN values >> datas = [T R]'; >> save mydatafile datas;
padr is a command from the blockset. It allows removing the NaN from the Rn matrix. The resulting R matrix is transposed and time is added in its first line. The time T which is a modified copy of t_Rn is not accurate since it is estimated by the time at which values are received. We know that the data are sent at a 1Khz frequency so we can redefine the time of the AxelX_GyroY_AxelZ matrix before saving the file.
Keep in mind than missing data on columns [2 3 4 5] are stuffed with their previous non missing value. Missing data on column 1 suppressed the time step. In other word, datas are incomplete and should not feed a simulink simulation. If we decided to log 3 data only (2 accelerometers and 1 gyro), all data would be received (9 bytes sent each time step). However, another method described below allows logging all the 5 values at 1kHz without missing any data!
Using the UART Tx Output block

The UART at 115200 can transmit only 11,52 data within a 1ms time-step. Thus, the simulink model implemented on the dsPIC must transmit less than 12 data to have all data being sent. The method described is more complex but allow logging all 5 measurement without lost with a sampling rate of 1kHz.
5 values of 12 bits length must be sent. Each data is stored in a 2 data bytes length (16 bits) and the 5 values, thus 10 data byes are concatenated. One signature byte with the fixed 55 is sent first, before the 10 bytes frame and provides the synchronization reference. This signature is may also used to check that no data were lost (checking that 10 bytes are present between every 55 signature values).
From the matlab GUI interface >> rs232gui, data received are no more multiplexed with the Tx Output Multiplexed for Matlab-Labview block. The demultiplexing algorithm is switched off by pushing once the RAW button (bottom left of the graphical interface). The embedded script in the rs232gui interface should be cleared. The R vector contains the raw data stream received by the Serial port of the computer. Once the recording is finished, this R vector is saved (files Rawdatas*.mat). The script Extract_RawDatas.m load the saved R vector and extract the 5 values. The key part of the script is shown below.
R = reshape(R,11,n); % reshape : from vector to a matrix of 11 column
idxError = find(R(1,:) ~= 55) % Check data integrity
if ~isempty(idxError)
error('Data corrupted')
end
%% Reconstruct Raw data as received through the SPI bus
RawGyro_Y = R(2,:)*2^8 + R(3,:);
RawAccel_Y = R(4,:)*2^8 + R(5,:);
RawAccel_Z = R(6,:)*2^8 + R(7,:);
RawGyro_X = R(8,:)*2^8 + R(9,:);
RawAccel_X = R(10,:)*2^8 + R(11,:);
T = [0:.001:(length(RawGyro_Y)-1)*.001];
On the embedded simulink model, a mechanism allow to send data during a predefined time: The model embedded on the dsPIC send data only when the value variable60 is different from 0. This variable is changed through the UART using the same rs232gui graphical user interface with the send1 and send2 button. When receiving values [60 x], the embedded simulink model load the value x into the Simulink variable 'variable60'. The Simulink model decreases automatically this variable at a sampling rate of 1 second. This mechanism makes the user able to log data during a predefined time.
Data Analysis
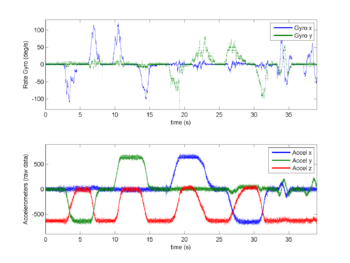
5 files corresponding to 5 different experiments are saved: 2 in static situation (IMU sensor board is keep static on the table) and 3 in dynamic situation while the IMU sensor board orientation is modified by a 90° rotation approximately every 5 seconds. The script Caracterisation_Capteurs.m plot the data previously saved for each different experiments.
Gain
The gain of the two rate gyro does not comply with the datasheet value. The datasheet give an angular speed rate of ±80°/s with a resolution of 0.039°/s. In practice, on the electronic sensor board, the Y rate gyro measures a range of ± 524°/s with a resolution of 0.26°/s. The X rate gyro can measure a range of ± 188°/s with a resolution of 0.09°/s.
the gain of the accelerometers is equal on all of the three axes and precise calibration is not necessary. A slight correction aligns the offset of each axis.
Noise
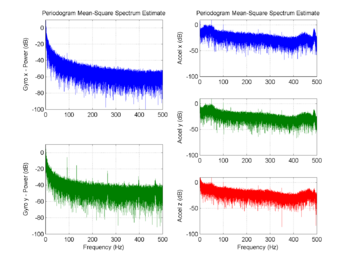
Figures RawData and RawDataSpectre show respectively the temporal and frequency analysis plot of the experiment stored in the Simulink_Dynamic_Calibration3.mat file.
This experiment is a dynamic one: with orientation changes. The temporal analysis shows that the rate gyro y axis contains more noise than the rate gyro x axis. This may be due to a soldering problem (It was very hard to sold all these parts with the very basic soldering material I have!), to a problem due to the ADIS16080 part itself or to the use of the y rate gyro ref voltage to power the accelerometer (that need a very low current). Anyway, the frequency analysis shows on the y rate gyro axis that this noise is mostly present within peaks frequency starting at 93Hz. As the gyro is integrated (integration act as a low pass filter) this high frequency noise has no influence on the angle estimation.
The frequency analysis also shows that the accelerometers are perturbed by the 50Hz component that probably comes from the European 50Hz general AC power. As the accelerometers is also low pass filtered, this high frequency noise has also no influence on the estimated angle.
Frequencies above 20Hz are considered as high frequency as the IMU is to be placed onboard a RC model airplane. The angular dynamic of theses aerial vehicle is far below 20Hz.
All files described can be downloaded (see bottom: Download section).
IMU Data fusion algorithms
Simulation with real data
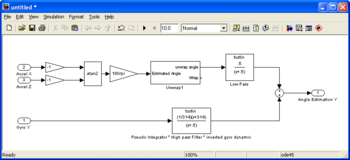
The model IMU_Simulation.mdl uses the logged data stored in .mat files. These data are used to design and simulate IMU algorithms. Using real data, the input of the simulation has the correct properties (noise, bias, nonlinearity...). The data stored are exactly the same data read at the output of sensors. Once the simulation provide correct results, the tuned algorithm is implemented as is (from simulink) directly in the microcontroller (PIC/dsPIC).
The raw data feeds the Sensor Calibration block. This block removes bias of rate gyro and accelerometers. Because we use the arctan function, the accelerometer axes do not need scaling. Only rate gyro measurements are scaled.
This Simulation compares Three angle estimation methods:
- Complementary filter (1st and 2nd order)
- Method described by Pisano 2005
- Non-adaptative Kalman filter
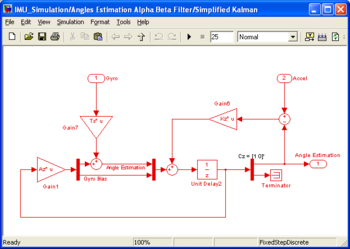
Complementary Filter
1st order
A complementary filter combines the angle estimations from both the rate gyro and the accelerometers. High frequency part of the angle estimated from the rate gyro is added to the low frequency part of the angle estimated with the accelerometers. Thus, the low drift of the estimated angle from the gyro is filtered out and only the high frequency part of the rate gyro estimated angle is retained. The low (or DC) frequency part of the angle estimated rely on the accelerometers angle estimation.
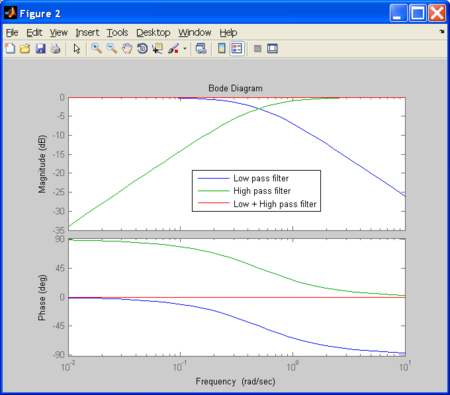
- The 0.08Hz first order low pass filter transfer function for the accelerometer is :
[math]Lp(s) = \frac{0.5}{s+0.5}[/math]
- The 0.08Hz first order High pass filter transfer function for the rate gyro is :
[math]Hp(s) = \frac{s}{s+0.5}[/math]
- From the analog device datasheet, the rate gyro has a cut off frequency at 40Hz. Thus, the transfer function of the integration of the rate gyro including the inverse dynamic of the rate gyro is:
[math]Int(s) = \frac{1}{314} * \frac{s+314}{s}[/math]
- For the rate gyro, we obtain the simplification :
[math]Hp(s) * Int(s) = \frac{s}{s+0.5} * \frac{1}{314} * \frac{s+314}{s} = \frac{1}{314} * \frac{s+314}{s+0.5}[/math]
The upper part of the complementary filter block estimates the Y axis angle computing the arctan of the X and Z accelerometers values. The lower part of the complementary filter blocks estimates the Y axis angle integrating the Y rate gyro. The dynamic of the gyro (low pass filter) is compensated for. The rate gyro is also high pass filtered to remove most of the DC part. The complementary filter, two first order filter (high pass and low pass) with cut off frequency at 0,08Hz. The final estimation of the angle is the addition of the resulting values from theses two filters.
This first order complementary filter gives fairly good results. However, the integrated rate gyro bias generates a ramp. The 1st order filter has a small steady state error while filtering the integrated rate gyro due to this ramp. An order 2 filter is however capable to remove this steady state error.
2nd order
We design a 2nd order complementary filter.
- The high pass filter is:
[math]Hp_2(s) = \frac{s^2}{(s+0.2)^2}[/math]
- The low pass filter is the complementary:
[math]Lp_2(s) = 1 - Hp_2(s) = \frac{0.4s + 0.02}{(s+0.2)^2}[/math]
- As for the 1st order complementary filter, the high pass filter can combine with the integration of the rate gyro. We do not take into account the dynamic of the rate gyro:
[math]\frac{1}{s} * \frac{s^2}{(s+0.2)^2} = \frac{s}{(s+0.2)^2}[/math]
This 2nd order complementary filter compensates for the rate gyro bias with no steady state error.
Method described by Pisano 2005
This method is not developed here but is given for completeness (see simulink files). The results are very similar to the order 1 complementary filter with the drawback of the steady state error due to the rate gyro bias estimation.
State Space Approach
The state space approach is equivalent to 2nd order complementary filter with the advantage of explicitly providing the estimated rate gyro bias and the unbiased angular rate of the system. The structure is a state space observer. The two states are the angle estimation and the gyro bias. The matlab function acker allows placing (through the gain K) the pole of the observer, defining the convergence of both the angle estimation and of the rate gyro bias. Defining a high speed convergence rate make the output more sensitive to the acceleration measurement, inducing noise from the accelerometers and sensitivity to the own acceleration of the unit that induce false angle estimation. A low convergence rate will make the bias estimation of the rate gyro very slow.
It is possible to set a different convergence rate for the two states. The gain K is static in this version. Using a variable gain K based on sensor noise measurement and system's own dynamic would result in the implementation of a Kalman Filter. However, added calculation are not worth because the characteristics of the system are fixed (Dynamic of the vehicle is fixe, and sensor noise is stationary). The gain obtained using a kalman filter does not justify its complexity.
Download
IMU_for_dsPIC.zip : All Simulink and Matlab file used with data logged. (updated on 21 september 2008)
The demo version of the blockset could compile model with up to 6 I/O pins. The Simulink model presented could not be compiled as is with the demo version of the blockset because SPI bus uses 5 pins and UART uses 2 pins (total is 7 pins). Removing the UART blocks, makes possible compiling theses models. Adding for example one PWM output may give the possibility to get the result for one angle.
Models name containing 'Simulation' are simulation of algorithm based on real data logged from the electronics. Models name without 'Simulation' are model that are directly compiled to generate an .hex file that can be downloaded into the microcontroller (Works with the registered version of the dsPIC blockset).
List of files:
- Simulink models
- IMU_Simulation.mdl
- IMU_Simulation_FxdPts.mdl
- IMU_dsPIC_30f4012_TestElectronics.mdl
- IMU_dsPIC_30f4012_LogData_Raw.mdl
- IMU_dPIC_30f4012_LogData_Multiplexed.mdl
- IMU_dsPIC_30f4012_ComplementaryFilter_20Mips.mdl
- IMU_dsPIC_30f4012_AlphaBetaFilter_20Mips.mdl
- IMU_dsPIC_30f4012_AlphaBetaFilter_20Mips_FixedPoints.mdl
- m script
- Extract_RawDatas.m
- Script_Kalman.m
- RealTimeVisualisationScript.m
- Caracterisation_Capteurs.m
- mat files
- RawDatas_Dynamic_Calibration_40se.mat : Raw data received from the dsPIC
- mat files to feed simulink model file IMU_Simulation.mdl
- Simulink_Dynamic_Calibration.mat
- Simulink_Dynamic_Calibration2.mat
- Simulink_Dynamic_Calibration3.mat
- Simulink_Static.mat
- Simulink_Static_60s.mat
Implementation on a dsPIC
Complementary Filter Order 1
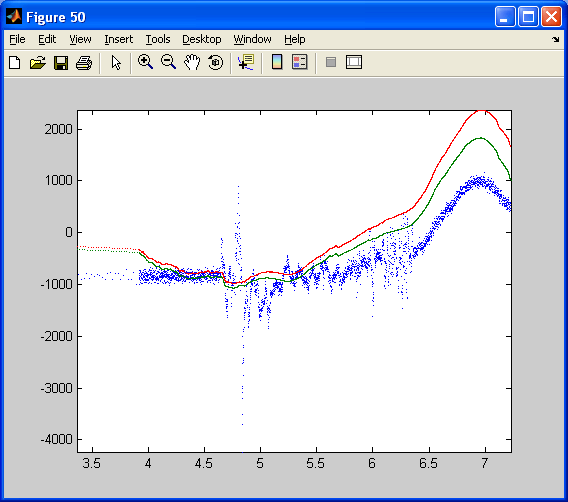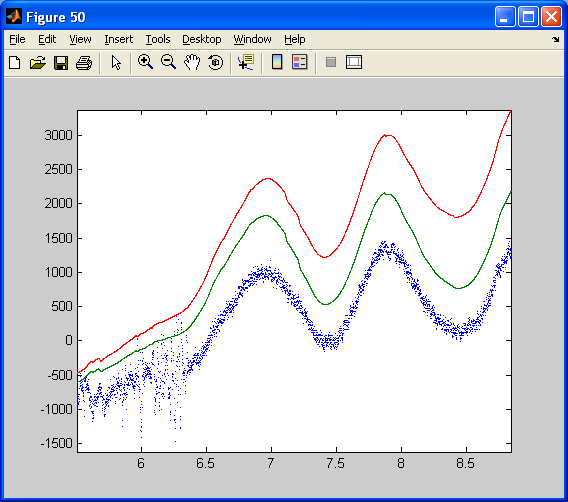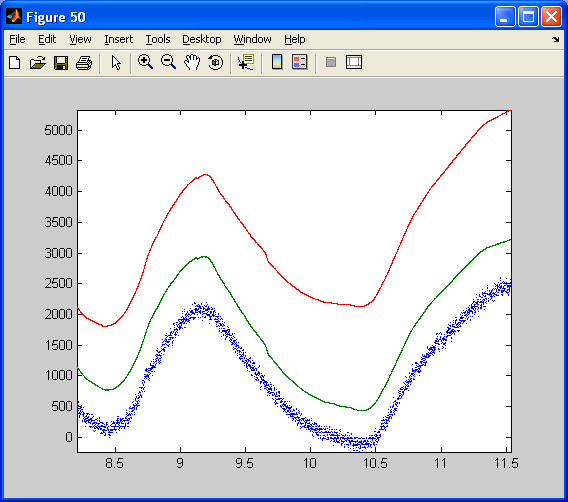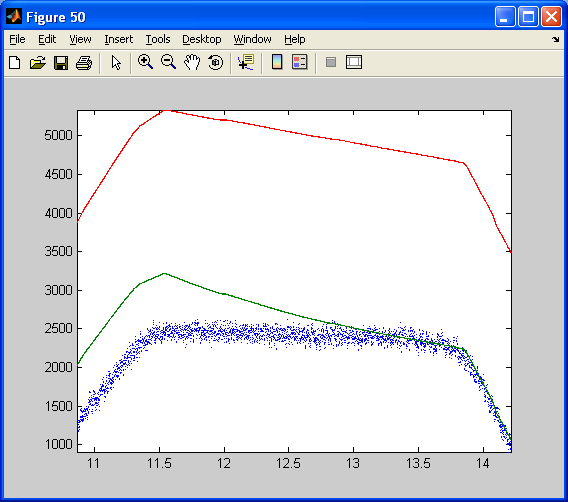
To design the filter for the dsPIC, the two precedent models are mixed up. The filter is inserted by copy-past into the first model used to log data. Data logged in real time from the complementary filter implemented on the dsPIC (30f4012 running at 10MHz). X axis: time in second. Y axis: angle multiplied by 100 (see model). The blue curve is the estimated angle from the X and Z accelerometers, resolving the gravity vector. The red curve is the estimated angle integrated from the Y rate gyro. The green curve is the angle estimated through the complementary filter that fusion the relevant information from both the Y axis rate gyro and the X and Z accelerometers.
The estimated angle using accelerometers (blue curve) is quite noisy. However, its steady value is correct. The estimated angle relying on the integration of the gyro is clean but drift (red curve). Note that the dsPIC has just been switch on and the High pass filter of the pseudo integrator of the gyro has not yet removed the remaining DC bias of the gyro. The DC bias of the Gyro has probably changed due to non constant temperature. Thus, the integrated angle drifts slowly from its real value. The green curves that use both data is clean and drift free. Its dynamics is as fast as the gyro dynamic. Note that at the beginning, the High pass filter (with a higher bandwidth than the gyro pseudo-integrator high pass filter) has not yet removed the gyro bias. However, at the end of the animation (11 seconds long: from 3, 5 to 14, 5), both curves (blue and green) are merging as in the simulation.
Fixed point
Fixed point version is working and can be downloaded in the .zip file at the bottom of the page.
IMU based on a 6 DoF sensor board (3 rate gyro, 3 accelerometers)
Limitations the IMU based on a 5DoF sensor board
The IMU based on the 5DoF sensor board have no rate gyro on the yaw axis. Thus, when the angular yaw rate is not null while the system is not horizontal, the pitch and roll angle of the system are modified despite the angular pitch and roll rate is 0! Thus, the pitch and roll angle estimation based on pitch and roll rate gyro is false, until the accelerometers information is taken into account and correct for the error (like a bias correction).
This problem is of particular concern when the IMU is used onboard a plane. When we decompose a plane change of flight direction:
- it takes a roll angle, then
- it rotates about both its pitch and yaw axis so as to keep its nose toward the horizon.
Thus, the pitch rate which tends to make the plane climbing is compensated for by the yaw rate that compensates and maintains plane heading aligned with the horizon. The IMU based of a 5DoF sensor board does not take into account the yaw rate. For a change of flight direction, the IMU measure a growing pitch angle despite (the plane is climbing) despite the true horizontal maintained by the plane.
Adaptation of the 5DoF IMU algorithm for a 6 DoF IMU
Electronic board evolution
The electronic sensor board is base on the electronic board presented above except than one rate gyro was added for measuring the yaw axis.
The added rate gyro had an unexpected effect; il changes most of the gain of the others rate gyro. Thus, the calibration was done again starting from scratch. Hopefully, the calibration had to be done only once because the sensors parameters do not changed.
Extended IMU algorithm
The algorithm used is an extension of the previous complementary filter algorithm. I used the state space approach.
Two version of the extended algorithm were done. The simpler one simply used exactly the same state space subsystem, but modified the two gyro input for both the pitch and roll input. The new pitch and roll input are a combination of both pitch and yaw or roll and yaw. The new pitch and roll input value for the subsystem (state space model) are the pitch and roll rotational rate in the earth frame of reference (in opposition to the previous plane frame of reference). The two rate angle were combined using trigonometric relation (cosine or sine) based on the current estimated angle. This method improved the results. However, the state space model estimation of the gyro bias is difficult as its input is now a combination of two rate gyro.
A second version was developed where the state space model were modified. In this last version, the state space model is capable to estimate a bias for the two rate gyro separately (all 3 rate gyro bias are estimated).
Theses new IMU algorithms take into account angle coupling and provide a correct attitude estimate.
All files of this 3 DoF IMU are provided as is.
IMU_2008_10_as_is.zip: All Simulink and Matlab file used with data logged for the 6DoF IMU. (Updated on 30 December 2008)
This IMU is being tested onboard a Remote Control (RC) flying wing. It is destined to become an important part of the autopilot currently under development. For more information, see page :
Acknowledgement
I would like to thanks companies that helped building this IMU by providing freely electronics components. Microchip provides microcontrollers and few others electronics parts. Analog Device provided samples of their great ADIS rate gyro part. Freescale also provide useful ds176 parts that acts like their MAX232 part but require less external component. Coil Craft provided really nice coil allowing to stabilize efficiently the sensor board's power lines.
Point to clarify, error, remarks? Please, leave your comment on the forum!