Blockset described on this wiki is deprecated since 2012.
For Model Based Design (MBD), use the free MPLAB Device Blocks for Simulink, tool from Microchip.
Updated Rapid Control Prototyping (RCP) custom projects are published at: https://lubin.kerhuel.eu.
Difference between revisions of "Miniature Inertial Measurement Unit - IMU"
LubinKerhuel (talk | contribs) |
LubinKerhuel (talk | contribs) |
||
| Line 1: | Line 1: | ||
| − | [[Image:IMU_Photo.jpg|thumb|right|250px|IMU sensors : 1 accelerometer MMA7260 from freescale (3 axis) coupled with 2 | + | [[Image:IMU_Photo.jpg|thumb|right|250px|IMU sensors : 1 accelerometer MMA7260 from freescale (3 axis) coupled with 2 rate gyros ADIS16080 from analog device (1 axis each) ]] |
| − | An Inertial Measurement Unit is based on inertial sensors to estimate its absolute angle also called atitude | + | A DIY Miniature Inertial Measurement Unit implemented on a dsPIC with a rapid prototyping tool. |
| − | The micro-Inertial Measurement Unit (IMU) presented here estimates its atitude around two rotation angles. The three principal components are: | + | |
| + | An Inertial Measurement Unit is based on inertial sensors to estimate its absolute angle in space also called atitude. | ||
| + | |||
| + | =Introduction= | ||
| + | |||
| + | The micro-Inertial Measurement Unit (IMU) presented here estimates its atitude around two rotation angles only: pitch and roll. The three principal components are: | ||
*2 one axis MEMS rate gyro measuring roll and pitch speed rate | *2 one axis MEMS rate gyro measuring roll and pitch speed rate | ||
*1 tri axial MEMS accelerometer measuring both the IMU acceleration and the gravity | *1 tri axial MEMS accelerometer measuring both the IMU acceleration and the gravity | ||
*1 dsPIC (30f or 33f) or 1 PIC24 | *1 dsPIC (30f or 33f) or 1 PIC24 | ||
| − | The atitude of the IMU system is | + | The atitude of the IMU system is estimated using information from the rate gyros and the accelerometers. |
| + | |||
| + | After a quick description of the angle estimation using accelerometers or gyro, this document describe the electronics board and explain how logging data throught the UART port of the PC. Then, the document presents the different estimation methods that fuse data from gyros and accelerometers to retrieve the atitude of the IMU system: | ||
*Complementary filter | *Complementary filter | ||
* non-adaptative Kalman filter | * non-adaptative Kalman filter | ||
| − | + | Simulink simulation of theses two methods, relying on real data previously logged, provide an easy way to tune each method, and to compare their efficiency. Once tuned, one method is implemented in the embedded PIC or dsPIC microcontroller in no time with the one push button method: the rapid prototyping tool described on this website (dsPIC blockset for Simulink). | |
| + | |||
=Problems of estimating angles from inertial sensors = | =Problems of estimating angles from inertial sensors = | ||
| + | |||
==Estimating angles from rate gyro== | ==Estimating angles from rate gyro== | ||
| − | A rate gyro measures its angular speed rate. Low noise and high precision of theses MEMS sensors are good | + | A rate gyro measures its angular speed rate. Low noise and high precision of theses MEMS sensors are very good. Thus, integrating the value of the rate gyro over time provide a good estimation of the angular displacement. Provided the initial position of the system is known and the sensor is ideal, the integration would provides the correct angular orientation. The integration function also acts as a low pass filter. The sensor noise, which is already low, is even lowered by this integration. |
| − | + | ||
| − | *<Tex>\Theta</Tex> the absolute pitch angle and '''q''' the pitch angular rate. <Tex>\hat \Theta = \ | + | Unfortunately, the rate gyro sensor is not ideal. Integrating the rate gyro also integrate its DC value. The integration of any error induced an unrecoverable bias on the estimated angle. As this DC value drifts slowly over time, it is not possible to cancel it by subtracting to the gyro output its DC offset value. Thus, a typically integration of a gyro would result in an angle drift of about 1° within one minute (depending on the rate gyro used!). It is necessary to use another sensor so as to recover the bias introduced by the integration of errors. |
| − | *<Tex>\Phi</Tex> the absolute roll angle and '''p''' the roll angular rate. <Tex>\hat \Phi = \ | + | *<Tex>\Theta</Tex> the absolute pitch angle and '''q''' the pitch angular rate. |
| + | <Tex>\hat \Theta(t) = \int_{t_0}^t{q(t) dt}+\Theta(t_0)</Tex> | ||
| + | *<Tex>\Phi</Tex> the absolute roll angle and '''p''' the roll angular rate. | ||
| + | <Tex>\hat \Phi(t) = \int_ t_0^t{p(t) dt} + \Phi(t_0)</Tex> | ||
| + | |||
==Estimating angles from accelerometers== | ==Estimating angles from accelerometers== | ||
| − | Accelerometers sense the both the gravity vertical acceleration vector (9.81m/s) added | + | Accelerometers sense the both the gravity vertical acceleration vector (9.81m/s) added to the acceleration of the sensor itself. Accelerometers are usually quite noisy and needs to be filtered. The acceleration of a system could in many case considered as small compared to the gravity acceleration value. If the system is considered as not accelerating (Hovering helicopters, flying gliders in stable straight flight...), it is possible to extract the pitch and roll absolute angle using the measured gravity vector. |
| + | |||
*ax the acceleration measured with the accelerometer on the x axis (longitudinal) | *ax the acceleration measured with the accelerometer on the x axis (longitudinal) | ||
*ay the acceleration measured with the accelerometer on the y axis (lateral) | *ay the acceleration measured with the accelerometer on the y axis (lateral) | ||
*az the acceleration measured with the accelerometer on the z axis (vertical) | *az the acceleration measured with the accelerometer on the z axis (vertical) | ||
| + | |||
Using the acceleration vector (i.e. gravity) measured with the accelerometers, we get the <Tex>\Theta</Tex> and <Tex>\Phi</Tex> angles : | Using the acceleration vector (i.e. gravity) measured with the accelerometers, we get the <Tex>\Theta</Tex> and <Tex>\Phi</Tex> angles : | ||
| + | |||
*<Tex>\hat \Theta= \arctan \left( \frac{a_z}{a_x} \right)</Tex> | *<Tex>\hat \Theta= \arctan \left( \frac{a_z}{a_x} \right)</Tex> | ||
*<Tex>\hat \Phi = \arctan \left( \frac{a_z}{a_y} \right)</Tex> | *<Tex>\hat \Phi = \arctan \left( \frac{a_z}{a_y} \right)</Tex> | ||
| − | |||
| − | |||
| − | |||
| − | ==Estimating angles from both | + | Note than when the axis az and ay are in the horizontal plane, the result is undefined. But pitch or roll angle is not defined as well (think of a plane which has its nose in the sky, perpendicular to the horizontal. Its absolute roll angle is undefined). |
| + | Absolute calibration of the accelerometers gain is not necessary because a rapport is calculated. The only point to care about is the offset of the three axes and the gain that must be the same for all three axes. | ||
| + | |||
| + | However, the first weakness of the angle estimated from accelerometers is its sensbility to the acceleration of the system. In others words, the estimated angle is biased whenever the system accelerates. The second weakness is the noisy result due to the accelerometers sensors. | ||
| + | |||
| + | ==Estimating angles from both rate gyro and Accelerometers== | ||
| + | |||
| + | Angle estimation from either a rate gyro or an accelerometers only do not provide good results. The characteristics of these two types of sensors are complementary: | ||
| − | |||
* Gyros provide a clean estimation of angle in dynamic situation on a short range time | * Gyros provide a clean estimation of angle in dynamic situation on a short range time | ||
* Accelerometers provide a noisy but absolute angle reference in static situation | * Accelerometers provide a noisy but absolute angle reference in static situation | ||
| − | It is therefore possible choose a data fusion algorithm so as to coupled the static reference angle from computed from the Accelerometers with the dynamic and clean angle variation estimation computed from the | + | |
| + | It is therefore possible choose a data fusion algorithm so as to coupled the static reference angle from computed from the Accelerometers with the dynamic and clean angle variation estimation computed from the rate gyro. | ||
| + | |||
=Embedded Electronics= | =Embedded Electronics= | ||
| − | |||
| − | |||
| − | |||
| − | The | + | [[Image:IMU_SensorSchematic.png|thumb|right|350px|This IMU use three MEMS sensors : One Three axial accelerometer (analog) and two one axis rate gyro with SPI interface. The 3 axes accelerometer MMA7260QT is powered by the 2.5V analog output reference created by the 'Y axis' rate gyro]] |
| − | =Log | + | The Embedded IMU Schematic is equipped with 1 accelerometer (3 axis) coupled with 2 rate gyro (1 axis each). |
| − | ==Using the UART | + | |
| − | [[Image: | + | One of the gyro supplies the 2.5V alimentation required by the accelerometer. Each gyro has two analog input pin connected to its internal ADC. Thus, the two gyros convert the three analog values of ax, ay, and az from the accelerometer. The IMU transmit the 5 data (3 acceleration + 2 rate gyros) to the microcontroller through a SPI bus. |
| + | |||
| + | The dsPIC:used (dsPIC 30f4012) is equipped with a 10Mhz quartz. This quartz frequency allows using the UART at 115200bps which is the max baud rate available on most personal computers (Serial port's limitation). | ||
| + | |||
| + | =Log raw data from sensor for simulink simulation= | ||
| + | |||
| + | Data from the inertial sensors are logged with matlab. Theses real data feeds a simulink model giving the possibility to develop/debug/compare different angle estimation algorithm. | ||
| + | |||
| + | All sensor data are received through the SPI peripheral of the dsPIC. Data are received from the two gyros using the [[/SPI_Input_Output_Interrupt_Driven|SPI Input/Output interrupt driven]] block. The code generated by this block use interrupt to constantly pool the two gyros and obtain the data. The output of the block is the most recent data received (for each requested data). | ||
| + | |||
| + | Data are transmitted through the UART peripheral. We have the following constraints: | ||
| + | * model time-step is 1ms | ||
| + | * UART speed rate is 115200bps | ||
| + | * 5 values of 12 bits resolution must be transmitted | ||
| + | |||
| + | Two methods to log datas are explained: The first logging method use the [[/Tx_Output_Multiplexed_For_Matlab-Labview|Tx Output Multiplexed for Matlab-Labview]] block. The other method use the [[/Tx_Output|Tx Output]] block. | ||
| + | Both logging method use the graphical matlab interface developed: [[/Interface_Tx-Matlab|Interface Tx-Matlab]] | ||
| + | |||
| + | |||
| + | ==Using the UART [[/Tx_Output_Multiplexed_For_Matlab-Labview|Tx Output Multiplexed for Matlab-Labview]] block == | ||
| + | |||
| + | [[Image:IMU_dsPIC_30f4012_TestElectronics.png|thumb|right|350px|''' IMU_dsPIC_30f4012_TestElectronics''' Simulink model: Once this model is compiled, the dsPIC (30f4012) transmit the values from the X, Y and Z axis of the accelerometer, and the Y and X axis of the rate gyro. Data are sent to Matlab (or labview) through the UART at 115200bps with the [[/Tx_Output_Multiplexed_For_Matlab-Labview|Tx Output Multiplexed for Matlab-Labview]] block. All data can not be send ; there will be missing data thus this model is usefull to check every component is working only.]] | ||
The model IMU_LogData is compiled and the generated .hex file is loaded into the dsPIC (using the bootloader [http://www.etc.ugal.ro/cchiculita/software/picbootloader.htm tinybld]). | The model IMU_LogData is compiled and the generated .hex file is loaded into the dsPIC (using the bootloader [http://www.etc.ugal.ro/cchiculita/software/picbootloader.htm tinybld]). | ||
| − | The model | + | The model samples the data at 1kHz, corresponding to the time-step of 1ms. During 1ms, the UART can send 11,52 Bytes when configured at 115200 bps (taking into account the start and stop bits). We log 5 int16 data that correspond to 10 bytes. The multiplexing protocol of the [[/Tx_Output_Multiplexed_For_Matlab-Labview|Tx Output Multiplexed for Matlab-Labview]] block.]] adds one byte for each variable sent. Thus, the model send 15 bytes at each time step. Because the model sends more than 11 data by time-step, some data will be lost. The Intelligent Spreading option will spread the lost over all data allowing to view all data on the graph (If not checked, the two last data may never be sent). |
| − | The data that get out from the | + | |
| − | The dsPIC is connected to the PC COM port ( | + | Because of the lost of some data, it is OK for plotting data and allows checking than all components are working. It is Not OK to use theses data as input data in a Simulink simulation! (You may however interpolate the data…) |
| − | >> [R T] = [[padr]](Rn,1,t_Rn); | + | |
| − | >> | + | The data that get out from the [[/Tx_Output_Multiplexed_For_Matlab-Labview|Tx Output Multiplexed for Matlab-Labview]] block are the sensor raw data. It is 16 bits data but only the 12 lower bits contains the measured value. |
| − | >> | + | |
| − | + | The dsPIC is connected to the PC COM port (using an equivalent to Max232 component for level translation) and data are logged using the [[Block/Interface_Tx-Matlab|graphical user interface]]. The following lines are typed at the maltab prompt to save data into a .mat file : | |
| − | [[padr]] is a command from the blockset. It allows | + | >> [R T] = [[padr]](Rn,1,t_Rn); % remove NaN values |
| + | >> datas = [T R]'; | ||
| + | >> save mydatafile datas; | ||
| + | |||
| + | The file obtained here can be used in simulink, however one must keep in mind than missing data on columns [2 3 4 5] are stuffed with their previous non missing value. Missing data on column 1 suppressed the time step. In other word, data is corrupted and should not be used in simulation. | ||
| + | If we decided to log 3 datas only (2 accelerometers and 1 gyro), all data would have been received (9 bytes per time step). The resulting file would have been usefull for a simulink simulation. However, the method described below allow to log the 5 datas without missing data! | ||
| + | |||
| + | [[padr]] is a command from the blockset. It allows removing the NaN from the Rn matrix. The resulting R matrix is transposed and time is added in its first line. The time T which is a modified copy of t_Rn is not accurate since it is estimated by the time at which values are received. We know that the data are sent at a 1Khz frequency so we can redefine the time of the AxelX_GyroY_AxelZ matrix before saving it into the AxelX_GyroY_AxelZ3.mat file. | ||
| + | |||
| + | ==Using the UART [[/Tx_Output|Tx Output]] block == | ||
| + | |||
| + | [[Image:IMU_dsPIC_30f4012_LogData_Raw.png|thumb|right|350px|''' IMU_dsPIC_30f4012_LogData_Raw ''' Simulink model: Once this model is compiled, the dsPIC (30f4012) transmit the values from the mems sensors. Data are sent to Matlab (or labview) through the UART at 115200bps with the [[/Tx_Output|Tx Output]] block. All data are sent making the logged data complete and useful for feed a simulink simulation.]] | ||
| + | |||
| + | The UART at 115200 can transmit only 11,52 data in a 1ms time-step. Thus, the simulink model implemented on the dsPIC must transmit less or equal 11 datas to be sure that there will be no data lost. | ||
| + | |||
| + | 5 data with 12 significant bits must be transmitted. The solution used code each data into 2 data bytes. One byte with the value 55 sent first is sent before the 10 frame bytes of the model to provide a synchronization reference. This byte may also be used to check that no data were lost (checking that 10 bytes are present between two 55 values). | ||
| + | |||
| + | No use multiplexing ==> use Raw data on Rs232gui | ||
| + | Data are sent when the variable60 gets a no null value… | ||
| + | Matlab Script description | ||
| − | |||
| − | |||
==Simulation based on real data== | ==Simulation based on real data== | ||
Angle estimation fusing rate gyro data with accelerometer data: A complementary filter combines the two estimation. High frequency part of the angle estimated from the rate gyro is added to the low frequency part of the angle estimated with the accelerometer. Thus, the low drift of the estimated angle from the gyro is filtered and only high frequency estimated angle from the gyro is used. The low frequency part of the angle estimated rely on the angle estimated using the accelerometer. The high frequency of the angle is estimated with the gyro which provide a fast and accurate information but which cannot be integrated due to the accumulation of the bias error. | Angle estimation fusing rate gyro data with accelerometer data: A complementary filter combines the two estimation. High frequency part of the angle estimated from the rate gyro is added to the low frequency part of the angle estimated with the accelerometer. Thus, the low drift of the estimated angle from the gyro is filtered and only high frequency estimated angle from the gyro is used. The low frequency part of the angle estimated rely on the angle estimated using the accelerometer. The high frequency of the angle is estimated with the gyro which provide a fast and accurate information but which cannot be integrated due to the accumulation of the bias error. | ||
| Line 65: | Line 121: | ||
[[Image:IMU_simu_RealData_Curves.png|frame|center|Top curves : The X (yellow) and Z (cyan) accelerometers raw data with the Y axis rate gyro (pink). The y scale is the raw numerical value as read from the Gyro-SPI bus. The x scale is time (simulation duration is 33,32s). | [[Image:IMU_simu_RealData_Curves.png|frame|center|Top curves : The X (yellow) and Z (cyan) accelerometers raw data with the Y axis rate gyro (pink). The y scale is the raw numerical value as read from the Gyro-SPI bus. The x scale is time (simulation duration is 33,32s). | ||
The three bottom curves are the simulated estimation of the angle (Y axis) using three different methods. The yellow curve is the estimated angle from the X and Z accelerometers, sensing the gravity. The cyan curve is the estimated angle, integrated from the Y rate gyro. The pink curve is the estimated angle estimated with the complementary filter that fusion the relevant information from both the Y rate gyro and the X-Z accelerometer]] | The three bottom curves are the simulated estimation of the angle (Y axis) using three different methods. The yellow curve is the estimated angle from the X and Z accelerometers, sensing the gravity. The cyan curve is the estimated angle, integrated from the Y rate gyro. The pink curve is the estimated angle estimated with the complementary filter that fusion the relevant information from both the Y rate gyro and the X-Z accelerometer]] | ||
| + | |||
==Complementary Filter== | ==Complementary Filter== | ||
| + | |||
[[Media:IMU_With_dsPIC.zip|Download]] the three models described above here with sample of sensor's data. | [[Media:IMU_With_dsPIC.zip|Download]] the three models described above here with sample of sensor's data. | ||
The aim of this complementary filter is to provide a method to implement a model on the dsPIC that has been previously improved thanks to the simulation capabilities of simulink. Simulation uses real data logged with the dsPIC peripheral (same electronic circuit, noise etc...) | The aim of this complementary filter is to provide a method to implement a model on the dsPIC that has been previously improved thanks to the simulation capabilities of simulink. Simulation uses real data logged with the dsPIC peripheral (same electronic circuit, noise etc...) | ||
In a first step, the real data are logged by the first model IMU_LogData. The complementary filter is simulated using the real data in the IMU_simu_RealData. The resulting model is then implemented into the dsPIC in the IMU_ComplementaryFilter model. | In a first step, the real data are logged by the first model IMU_LogData. The complementary filter is simulated using the real data in the IMU_simu_RealData. The resulting model is then implemented into the dsPIC in the IMU_ComplementaryFilter model. | ||
| + | |||
===Complementary Filter running on dsPIC === | ===Complementary Filter running on dsPIC === | ||
| + | |||
[[Image:IMU_ComplementaryFilter.png|thumb|right|350px|The IMU_ComplementaryFilter simulink model is a 'copy-past' mixture made of the IMU_LogData 'data management' part with the IMU_simu_RealData model tuned and optimize filter. This model implements the complementary filter on the dsPIC and sends the result to matlab. It will have the same behaviors of the simulated filter.]] | [[Image:IMU_ComplementaryFilter.png|thumb|right|350px|The IMU_ComplementaryFilter simulink model is a 'copy-past' mixture made of the IMU_LogData 'data management' part with the IMU_simu_RealData model tuned and optimize filter. This model implements the complementary filter on the dsPIC and sends the result to matlab. It will have the same behaviors of the simulated filter.]] | ||
To design the filter for the dsPIC, the two precedent models are mixed up. The filter is inserted by copy-past into the first model used to log data. | To design the filter for the dsPIC, the two precedent models are mixed up. The filter is inserted by copy-past into the first model used to log data. | ||
| Line 92: | Line 152: | ||
Programming dsPIC or PIC24 becomes exciting and fun with this toolbox. You do not have to waste your time with configuration of the dsPIC peripherals! Focus only on simulink simulation, Real time Workshop capabilities, and on fixed point optimization. | Programming dsPIC or PIC24 becomes exciting and fun with this toolbox. You do not have to waste your time with configuration of the dsPIC peripherals! Focus only on simulink simulation, Real time Workshop capabilities, and on fixed point optimization. | ||
| − | = | + | =On-going projects= |
| − | I am planning to | + | I am planning to use this IMU in an autopilote for remote controlled glider ( as previous project described on my french website : http://lubink.free.fr) |
Point to clarify, error, remarks ? Please, leave your comment on the forum ! | Point to clarify, error, remarks ? Please, leave your comment on the forum ! | ||
| + | |||
| + | |||
[[Category:Example]] | [[Category:Example]] | ||
Revision as of 19:54, 11 July 2008
A DIY Miniature Inertial Measurement Unit implemented on a dsPIC with a rapid prototyping tool.
An Inertial Measurement Unit is based on inertial sensors to estimate its absolute angle in space also called atitude.
Contents
Introduction
The micro-Inertial Measurement Unit (IMU) presented here estimates its atitude around two rotation angles only: pitch and roll. The three principal components are:
- 2 one axis MEMS rate gyro measuring roll and pitch speed rate
- 1 tri axial MEMS accelerometer measuring both the IMU acceleration and the gravity
- 1 dsPIC (30f or 33f) or 1 PIC24
The atitude of the IMU system is estimated using information from the rate gyros and the accelerometers.
After a quick description of the angle estimation using accelerometers or gyro, this document describe the electronics board and explain how logging data throught the UART port of the PC. Then, the document presents the different estimation methods that fuse data from gyros and accelerometers to retrieve the atitude of the IMU system:
- Complementary filter
- non-adaptative Kalman filter
Simulink simulation of theses two methods, relying on real data previously logged, provide an easy way to tune each method, and to compare their efficiency. Once tuned, one method is implemented in the embedded PIC or dsPIC microcontroller in no time with the one push button method: the rapid prototyping tool described on this website (dsPIC blockset for Simulink).
Problems of estimating angles from inertial sensors
Estimating angles from rate gyro
A rate gyro measures its angular speed rate. Low noise and high precision of theses MEMS sensors are very good. Thus, integrating the value of the rate gyro over time provide a good estimation of the angular displacement. Provided the initial position of the system is known and the sensor is ideal, the integration would provides the correct angular orientation. The integration function also acts as a low pass filter. The sensor noise, which is already low, is even lowered by this integration.
Unfortunately, the rate gyro sensor is not ideal. Integrating the rate gyro also integrate its DC value. The integration of any error induced an unrecoverable bias on the estimated angle. As this DC value drifts slowly over time, it is not possible to cancel it by subtracting to the gyro output its DC offset value. Thus, a typically integration of a gyro would result in an angle drift of about 1° within one minute (depending on the rate gyro used!). It is necessary to use another sensor so as to recover the bias introduced by the integration of errors.
- <Tex>\Theta</Tex> the absolute pitch angle and q the pitch angular rate.
<Tex>\hat \Theta(t) = \int_{t_0}^t{q(t) dt}+\Theta(t_0)</Tex>
- <Tex>\Phi</Tex> the absolute roll angle and p the roll angular rate.
<Tex>\hat \Phi(t) = \int_ t_0^t{p(t) dt} + \Phi(t_0)</Tex>
Estimating angles from accelerometers
Accelerometers sense the both the gravity vertical acceleration vector (9.81m/s) added to the acceleration of the sensor itself. Accelerometers are usually quite noisy and needs to be filtered. The acceleration of a system could in many case considered as small compared to the gravity acceleration value. If the system is considered as not accelerating (Hovering helicopters, flying gliders in stable straight flight...), it is possible to extract the pitch and roll absolute angle using the measured gravity vector.
- ax the acceleration measured with the accelerometer on the x axis (longitudinal)
- ay the acceleration measured with the accelerometer on the y axis (lateral)
- az the acceleration measured with the accelerometer on the z axis (vertical)
Using the acceleration vector (i.e. gravity) measured with the accelerometers, we get the <Tex>\Theta</Tex> and <Tex>\Phi</Tex> angles :
- <Tex>\hat \Theta= \arctan \left( \frac{a_z}{a_x} \right)</Tex>
- <Tex>\hat \Phi = \arctan \left( \frac{a_z}{a_y} \right)</Tex>
Note than when the axis az and ay are in the horizontal plane, the result is undefined. But pitch or roll angle is not defined as well (think of a plane which has its nose in the sky, perpendicular to the horizontal. Its absolute roll angle is undefined). Absolute calibration of the accelerometers gain is not necessary because a rapport is calculated. The only point to care about is the offset of the three axes and the gain that must be the same for all three axes.
However, the first weakness of the angle estimated from accelerometers is its sensbility to the acceleration of the system. In others words, the estimated angle is biased whenever the system accelerates. The second weakness is the noisy result due to the accelerometers sensors.
Estimating angles from both rate gyro and Accelerometers
Angle estimation from either a rate gyro or an accelerometers only do not provide good results. The characteristics of these two types of sensors are complementary:
- Gyros provide a clean estimation of angle in dynamic situation on a short range time
- Accelerometers provide a noisy but absolute angle reference in static situation
It is therefore possible choose a data fusion algorithm so as to coupled the static reference angle from computed from the Accelerometers with the dynamic and clean angle variation estimation computed from the rate gyro.
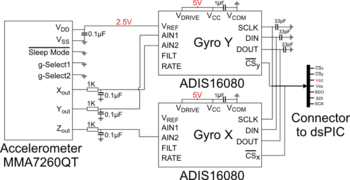
Embedded Electronics
The Embedded IMU Schematic is equipped with 1 accelerometer (3 axis) coupled with 2 rate gyro (1 axis each).
One of the gyro supplies the 2.5V alimentation required by the accelerometer. Each gyro has two analog input pin connected to its internal ADC. Thus, the two gyros convert the three analog values of ax, ay, and az from the accelerometer. The IMU transmit the 5 data (3 acceleration + 2 rate gyros) to the microcontroller through a SPI bus.
The dsPIC:used (dsPIC 30f4012) is equipped with a 10Mhz quartz. This quartz frequency allows using the UART at 115200bps which is the max baud rate available on most personal computers (Serial port's limitation).
Log raw data from sensor for simulink simulation
Data from the inertial sensors are logged with matlab. Theses real data feeds a simulink model giving the possibility to develop/debug/compare different angle estimation algorithm.
All sensor data are received through the SPI peripheral of the dsPIC. Data are received from the two gyros using the SPI Input/Output interrupt driven block. The code generated by this block use interrupt to constantly pool the two gyros and obtain the data. The output of the block is the most recent data received (for each requested data).
Data are transmitted through the UART peripheral. We have the following constraints:
- model time-step is 1ms
- UART speed rate is 115200bps
- 5 values of 12 bits resolution must be transmitted
Two methods to log datas are explained: The first logging method use the Tx Output Multiplexed for Matlab-Labview block. The other method use the Tx Output block. Both logging method use the graphical matlab interface developed: Interface Tx-Matlab
Using the UART Tx Output Multiplexed for Matlab-Labview block
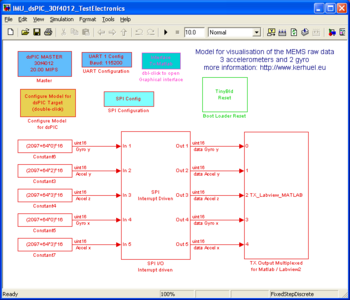
The model IMU_LogData is compiled and the generated .hex file is loaded into the dsPIC (using the bootloader tinybld). The model samples the data at 1kHz, corresponding to the time-step of 1ms. During 1ms, the UART can send 11,52 Bytes when configured at 115200 bps (taking into account the start and stop bits). We log 5 int16 data that correspond to 10 bytes. The multiplexing protocol of the Tx Output Multiplexed for Matlab-Labview block.]] adds one byte for each variable sent. Thus, the model send 15 bytes at each time step. Because the model sends more than 11 data by time-step, some data will be lost. The Intelligent Spreading option will spread the lost over all data allowing to view all data on the graph (If not checked, the two last data may never be sent).
Because of the lost of some data, it is OK for plotting data and allows checking than all components are working. It is Not OK to use theses data as input data in a Simulink simulation! (You may however interpolate the data…)
The data that get out from the Tx Output Multiplexed for Matlab-Labview block are the sensor raw data. It is 16 bits data but only the 12 lower bits contains the measured value.
The dsPIC is connected to the PC COM port (using an equivalent to Max232 component for level translation) and data are logged using the graphical user interface. The following lines are typed at the maltab prompt to save data into a .mat file :
>> [R T] = padr(Rn,1,t_Rn); % remove NaN values >> datas = [T R]'; >> save mydatafile datas;
The file obtained here can be used in simulink, however one must keep in mind than missing data on columns [2 3 4 5] are stuffed with their previous non missing value. Missing data on column 1 suppressed the time step. In other word, data is corrupted and should not be used in simulation. If we decided to log 3 datas only (2 accelerometers and 1 gyro), all data would have been received (9 bytes per time step). The resulting file would have been usefull for a simulink simulation. However, the method described below allow to log the 5 datas without missing data!
padr is a command from the blockset. It allows removing the NaN from the Rn matrix. The resulting R matrix is transposed and time is added in its first line. The time T which is a modified copy of t_Rn is not accurate since it is estimated by the time at which values are received. We know that the data are sent at a 1Khz frequency so we can redefine the time of the AxelX_GyroY_AxelZ matrix before saving it into the AxelX_GyroY_AxelZ3.mat file.
Using the UART Tx Output block

The UART at 115200 can transmit only 11,52 data in a 1ms time-step. Thus, the simulink model implemented on the dsPIC must transmit less or equal 11 datas to be sure that there will be no data lost.
5 data with 12 significant bits must be transmitted. The solution used code each data into 2 data bytes. One byte with the value 55 sent first is sent before the 10 frame bytes of the model to provide a synchronization reference. This byte may also be used to check that no data were lost (checking that 10 bytes are present between two 55 values).
No use multiplexing ==> use Raw data on Rs232gui Data are sent when the variable60 gets a no null value… Matlab Script description
Simulation based on real data
Angle estimation fusing rate gyro data with accelerometer data: A complementary filter combines the two estimation. High frequency part of the angle estimated from the rate gyro is added to the low frequency part of the angle estimated with the accelerometer. Thus, the low drift of the estimated angle from the gyro is filtered and only high frequency estimated angle from the gyro is used. The low frequency part of the angle estimated rely on the angle estimated using the accelerometer. The high frequency of the angle is estimated with the gyro which provide a fast and accurate information but which cannot be integrated due to the accumulation of the bias error.
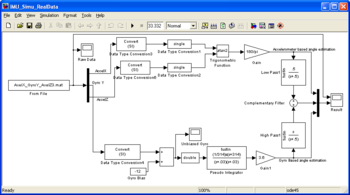
The model IMU_Simu_RealData uses the logged data contained in the file AxelX_GyroY_AxelZ3.mat. These data are used to design a simple complementary filter and simulate it. Because we are using real data, the input of the simulation has precisely the right properties (noise, bias...). The filter can be design and simulated with data that are close to reality. In this model, datas are converted back into their former fixed point representation data type. In other word, their binary data is not modified, but the scaling is modified. After the first conversion block, they are equivalent to the data of the IMU_sensors block of the previous model. Data are converted again into double or single to simplify the design at this step. The upper part of the model estimates the Y axis angle computing the atan of the X and Z accelerometers values. Because we use the Atan function, the two accelerometer axis do not need to be scaled. The only constraint is that the X and Z acceleration share the same scaling. The lower part of the model estimates the Y axis angle integrating the Y rate gyro. The dynamic of the gyro (low pass filter) is compensated for. The rate gyro is also high pass filtered to remove most of the DC part. The complementary filter, two first order filter (high pass and low pass) with cut off frequency at 0,08Hz. The final estimation of the angle is the addition of the resulting values from theses two filters. The result is presented in pink on the lower part of the following figure.
Complementary Filter
Download the three models described above here with sample of sensor's data. The aim of this complementary filter is to provide a method to implement a model on the dsPIC that has been previously improved thanks to the simulation capabilities of simulink. Simulation uses real data logged with the dsPIC peripheral (same electronic circuit, noise etc...) In a first step, the real data are logged by the first model IMU_LogData. The complementary filter is simulated using the real data in the IMU_simu_RealData. The resulting model is then implemented into the dsPIC in the IMU_ComplementaryFilter model.
Complementary Filter running on dsPIC
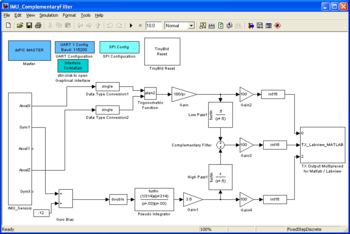
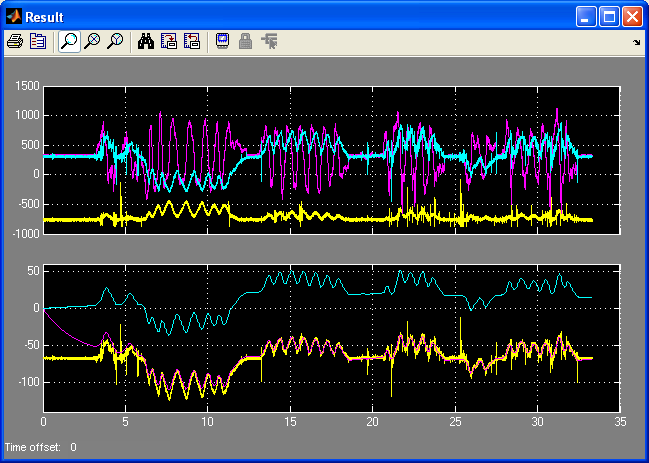
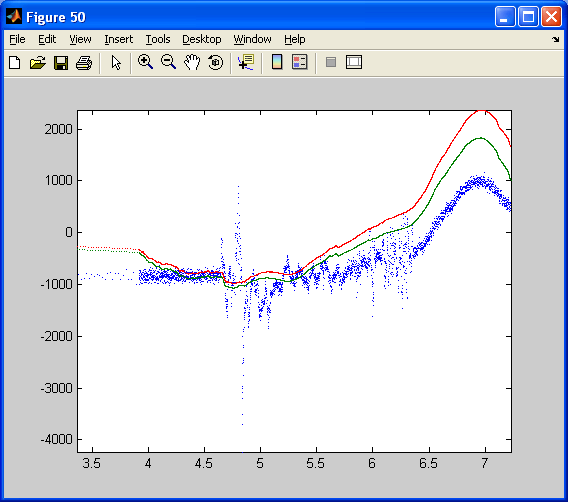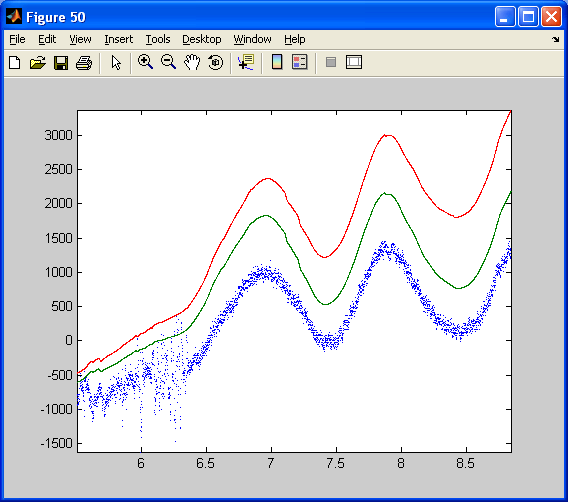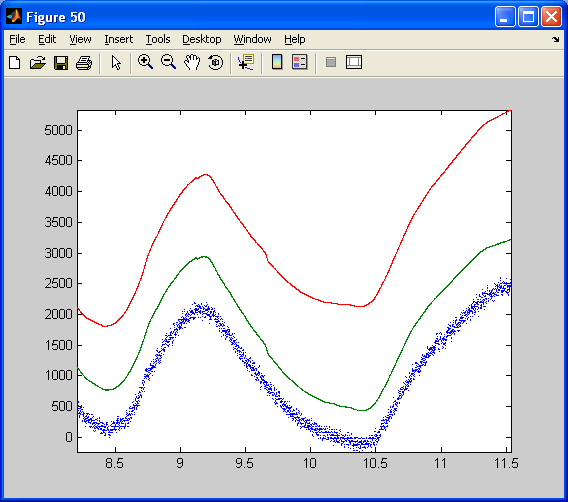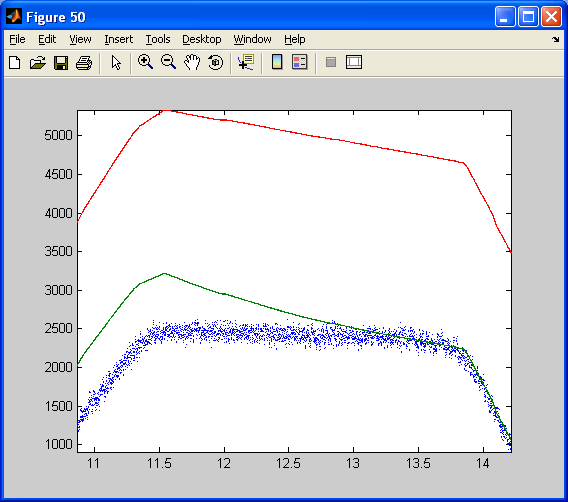
To design the filter for the dsPIC, the two precedent models are mixed up. The filter is inserted by copy-past into the first model used to log data. Data logged in real time from the complementary filter implemented on the dsPIC (30f4012 running at 10MHz). X axis : time in second. Y axis : angle multiplied by 100 (see model) The blue curve is the estimated angle from the X and Z accelerometers, resolving the gravity vector. The red curve is the estimated angle integrated from the Y rate gyro. The green curve is the angle estimated through the complementary filter that fusion the relevant information from both the Y axis rate gyro and the X and Z accelerometers.
The estimated angle using accelerometers (blue curve) is quite noisy. However, it steady value is correct. The estimated angle relying on the integration of the gyro is clean but drift (red curve). Note that the dsPIC has just been switch on and the High pass filter of the pseudo integrator of the gyro has not yet removed the remaining DC bias of the gyro. The DC bias of the Gyro has probably change due to non constant temperature in my house. (I do not have a clim in my tiny room which is in a roof in Marseille! ). Thus, the gyro integrated angle is slowing drifting away from its real value. The green curves that use both data is clean and drift free. Its dynamics is as fast as the gyro dynamic. Note that at the beginning, the High pass filter (with a higher bandwidth than the gyro pseudo-integrator high pass filter) has not yet removed the gyro bias. However, at the end of the animation (11 secondes long: from 3, 5 to 14, 5), both curves (blue and green) are merging as in the simulation.
Remarks about the complementary filter
The integration of the gyro should be done after the high-pass filter of the complementary filter. This filter placed before the integration would avoid getting high value in the integration internal computation. High value with floating point data mean that the calculation loses its precision. The high-pass filter of the complementary filter has been placed at the end for reason of simplicity and to compare easily the estimation of the angle with the three methods ( integrating gyro, using accelerometer, or by combining both).
All calculation are done in double data type or single data type. Theses float data slow down the calculation and use a large amount of memory. It is quite powerful with the help of simulink to build a fixed point complementary filter. Thus, next step is to go back to the simulation model and to design a fixed point complementary filter! (Using the matlab fixed point toolbox)
Alpha Beta Filter
coming soon
Conclusion
Programming dsPIC or PIC24 becomes exciting and fun with this toolbox. You do not have to waste your time with configuration of the dsPIC peripherals! Focus only on simulink simulation, Real time Workshop capabilities, and on fixed point optimization.
On-going projects
I am planning to use this IMU in an autopilote for remote controlled glider ( as previous project described on my french website : http://lubink.free.fr)
Point to clarify, error, remarks ? Please, leave your comment on the forum !